3. TOOLKIT DEMONSTRATION

MultiTaper Method

Having selected the data vector to be analyzed (here our 'soi' vector with the SOI time series) and the value of a sampling interval, a Default button is provided as a guide to set the rest of MTM parameters. By selecting the Coherence check box, user can choose another vector to compute MTM coherence with the Data vector. Both vectors should have the same length.

Results of MTM analysis, i.e. harmonic F-test, Spectrum or Coherence, are stored in a matrix with a name specified in Spectrum field. In addition, related MTM confidence levels (F-test, Spectrum or Coherence) are stored in a matrix with the name obtained by prefixing "conf_" to a Spectrum name, and can be accessed in Data I/O tool. If results from several MTM calculations have been stored in different matrices, the parameters used in a particular MTM analysis will be restored in GUI by simply selecting correspondent matrix from a Spectrum pop-up list.

Entering a new number in the `Resolution' box specifies the factor p in effective half-bandwidth resolution pf_n , where f_n=1/Ndt is the minimum possible spectral resolution from its default value p=2.

Entering a new value in the `Number of Tapers' box resets the number of windowing functions used in spectral estimation. This value cannot exceed the 2p-1 where p is the integer entered in the `Resolution' box. A lower value can however be set for `Number of Tapers' if the user wants to be especially conservative regarding potential spectral leakage bias.

``Signal' settings:

• All (default)
• Narrowband
• Hamonic

Option ``All'' indicates that MTM spectrum will be tested both for the presence of narrowband signals, whose significance is measured by their amplitude relative to the estimated noise background, and for the presence of ``harmonic'' signals, which are significant as measured by the Thomson variance ratio test for periodic signals (F-test). Spectral peaks that pass both tests simultenously will form the Reshaped spectrum (see below Advanced settings), and together with the Raw MTM spectral estimate are stored as results. Also, the frequencies of highly significant narrowband signals will be shown in MTM components table, that can be selected for subsequent Reconstruction.

Option``Narrowband'' will test the MTM spectrum only for the significance of narrowband signals using their amplitude relative to the estimated background of selected noise null-hypothesis in Significance settings, and no Reshaping procedure is performed.

Option``Harmonic'' will test the spectrum only for the presence of periodic signals, and the results of F-test and its confidence levels are stored as MTM results. MTM components table will contain frequencies of highly significant F-test signals that can be selected for subsequent Reconstruction.

``Significance'' settings:

• red noise (default)
• locally white
• white

The choice of ``red noise ''assumes a noise background that consists of a temporally integrated Gaussian white noise or ``AR(1)'' noise process. This null hypothesis is strongly motivated for dynamical reasons in the study of geophysical phenomena, and represents the default option of the Toolkit.

The choice of ``locally white noise'' assumes a colored noise process that varies slowly but arbitrarily with frequency. This choice is recommended if there is a priori reason to believe that the noise background has a complex structure.

The choice of ``white noise'' represents a good null hypothesis if absolutely nothing is known a priori about the physics or dynamics of the process producing the noise background.

Advanced Options

Here user can change various settings from their defaults, control MTM Plot Options, as well as reconstructing signal at selected significant frequencies.

.

The ``Spectrum'' settings:

• adaptive (default)
• high-resolution

The choice ``adaptive'' indicates that the adaptive MTM spectrum estimation procedure, most resistant to broadband spectral leakage, is to be employed. This is the default option.

The choice ``high-resolution'' indicates that the high-resolution MTM spectrum, involving a simple weighted average of the contributions of independent eigenspectra, should be calculated.

• N (default)
• none

The choice ``N'' represents a convention in which the spectrum is calculated per unit time by dividing by the length of the data series in time units ``N'' (ie, a power spectral density), the default convention throughout the Toolkit.

The choice ``none'' indicates a standard Fourier convention of a finite length time series in which the spectrum scales with the number of data points.

Here the user can change threshold for significance of harmonic peak detection (F-test , 90%,95%,99%,99.5% and 99.9%) used in the ``Reshaping'' procedure.

A ``Reshaping'' procedure is used to separate the continuous and harmonic portions of the spectrum, and is performed only when the Signal option is set to All. The detected harmonic peak will be reshaped only if it is ALSO significant to the estimated noise background at a F-test level. The ``Reshaping'' procedure is not performed if Narrowband option is selected.

The user should be aware that chance statistics should lead to a 5% rate of spurious harmonic signal detection at the 95% level, corresponding to roughly 2-3 false positives over the Nyquist interval for a time series of length N=100 time units, so that one should interpret with great caution significance of less than about 1-1/N.

The ``Noise'' settings:

The ``Robust'' choice for the noise background estimation employs a robust estimator (median smooth) to find an optimal background fit to the empirical spectrum for measuring the significance of narrowband signals. This choice guards against the contamination of noise parameter estimation by narrowband signal and significant trend contributions, and represents the default option.

The ``Raw'' option estimates noise parameters directly from the unfiltered or ``raw'' time series. This option, albeit more traditional, is generally discouraged. It should be selected, however, if the user is interested in signals whose significance is measured only by the Thomson variance ratio test for periodicity, without regard to their significance as measured by their amplitude relative to the estimated noise background.

The `Frequency Range' settings:

The `Frequency from' .. `To' .. ' values allow one to change the frequency range from its default value f=0 to f_N=0.5/dt, where dt is the sampling value entered by the user. Selected frequencies must fall within the Nyquist range or a warning is given. The selected frequency range will determine the frequency interval over which other options (e.g., median smoothing, robust red noise fit--see below) will operate. The number of frequencies over the interval f=0 to 0.5/dt is the first power of 2 greater than the number of data points, or 1024--whichever value is larger. The latter choice provides a visually smooth interpolated spectrum when the number of data points is small. A selected sub range will contain a proportionately smaller number of frequency points.

Please note that the null hypothesis is effectively re-determined whenever sub-interval of the spectrum is analyzed. In this case an AR(1) spectrum is fitted only to that range, which will in general change the confidence levels, and thus, potentially, the threshold for "reshaping" of the spectrum, and detecting a harmonic peak!

Here it is possible to modify the way that the ``robust'' noise background is estimated. The default is to select a noise background based on the fit to a median smooth of the raw spectrum. The median smoothing window width can be varied by the user within the range 2pf<sub>n</sub> to f<sub>N</sub>/4. This generally insures that the overall structure of the spectrum over the full ``Nyquist'' interval is recognized in the optimal background fit, while assuring that the fit is resistant to the influence of narrowband features in the spectrum.

In addition ``Misfit Criterion'' can be set to either a log fit or a linear fit:

The ``log fit'' employs a criterion which minimizes the misfit of the robustly estimated background with the log of the spectral density. This provides a better conceptual fit to the spectrum when dynamic ranges are large, and is the suggested choice. It is the default option.

The ``linear fit'' employs a criterion which will weight the robust fit of the noise background by the amplitude of the spectrum. This choice is recommended if it is more important to fit the low-frequency, high-power part of noise background. 

Any results which show great sensitivity to the choice of ``log fit'' and ``linear fit'', or to the value of the median smoothing window over that range should be interpreted with some caution.

MTM Components table:

This table will contain list of the frequencies of highly significant signals (greater than the 90% level ) either from MTM spectrum, MTM harmonic test or MTM coherence, which can be selected for subsequent MTM reconstruction.

If Signal option is set to All or Narrowband , the Components table will contain a list of the central frequencies of narrowband signals (with their significance) in the MTM spectral estimate, identified as significant relative to the specified null hypothesis. For the Harmonic option of Signal it will contain the ``harmonic'' signals which are significant as measured by MTM Harmonic test (F-test) for periodic signals.

A maximum of the 200 most significant signals are stored.

Plot Options:

User can choose to plot different types of spectra, as well as confidence levels (spectral, F-test or coherence) by pressing on Plot Options button of Advanced options window:

MTM Spectrum

To calculate the power spectrum of our SOI series, we set the parameter for the ``Reshape'' to 90%, and click the Compute button. Then, we click the Plot button to view the spectrum which should look like the following:

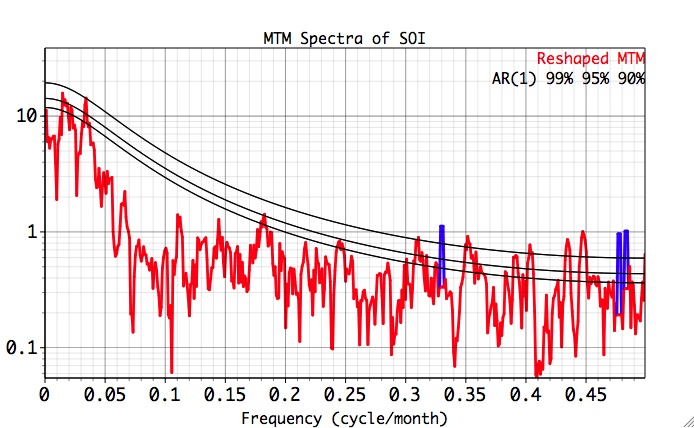
The above figure shows estimated continuous MTM spectrum or ``reshaped spectrum'' (the spectrum with estimated contributions of harmonic signals removed). Also, three additional smooth curves are shown, in increasing vertical progression, for the 90%, 95%, and 99% significance levels relative to the estimated noise background. Finally, the estimated harmonic or periodic component of the spectrum can be also displayed, i.e. the plot shows the estimated continuous spectrum, along with a curve that rises above it to indicate the portion of the spectrum above the continuous background associated with a period signal. The latter component is shown as a narrow spike of breadth equal to the spectral estimation bandwidth.

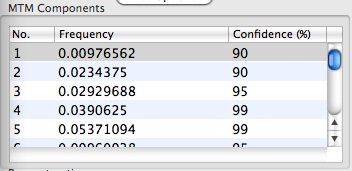
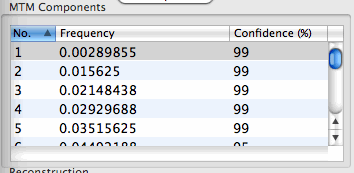
As we can see from the MTM Components table:

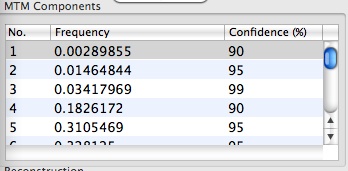
the MTM analysis identifies two highly significant peaks, one centered at f=0.0146, and another centered at f=0.0342. We associate these peaks with the low-frequency LF(band) and high frequency (HF) band ENSO signals. The blue peaks indicate harmonic signals selected in the Reshaping procedure.

MTM Harmonic F-test

Results of F-test for harmonic signals can be stored and plotted by performing MTM analysis with Harmonic option chosen in Signal settings:

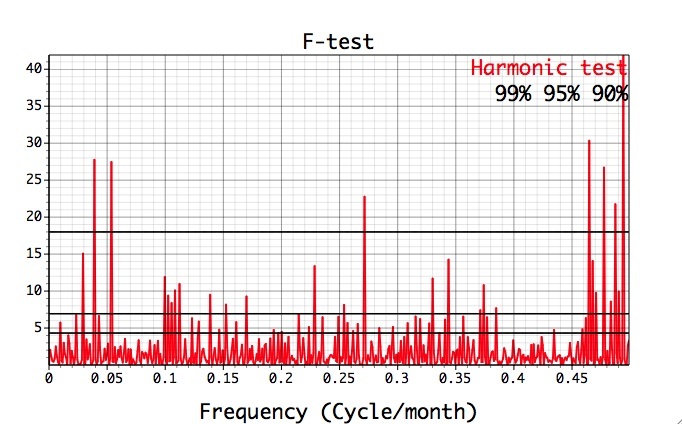
The list of F-test significant frequencies in the MTM Components table differs significantly from the narrowband signals:

which explains why no peaks have been reshaped in ENSO frequency band, and is another manifestation of the quasi-periodic nature of ENSO.

MTM Reconstruction

(Note: In a demo version, MTM Reconstruction is available only for data of example projects! For custom data this feature is enabled after activation with a purchased Serial No.)

The Components table on the MTM Advanced options panel allows the reconstruction of the original time series from selected frequencies by clicking the 'Compute' button in Reconstruction. The ``Plot'' button plots the sum of the reconstructed components against the original time series. The name of vector with reconstruction is specified by the user in Result field of Reconstruction box. Individual RC components are stored in matrix with name obtained by prefixing "mat_" to Result name, and can be accessed in Data I/O tool. If results from several reconstructions have been stored in different vectors, the parameters for a particular reconstruction will be restored in GUI by simply selecting correspondent vector from a Result pop-up list. Checking "fliter out" box will filter out the selected components from the original data; this option is quite useful for detrending.

After selecting significant MTM spectral frequencies, clicking the Compute and Plot buttons in Reconstruction box, and adjusting the plot settings in Graph Controls), we obtain the following MTM-filtered series:

MTM Coherence

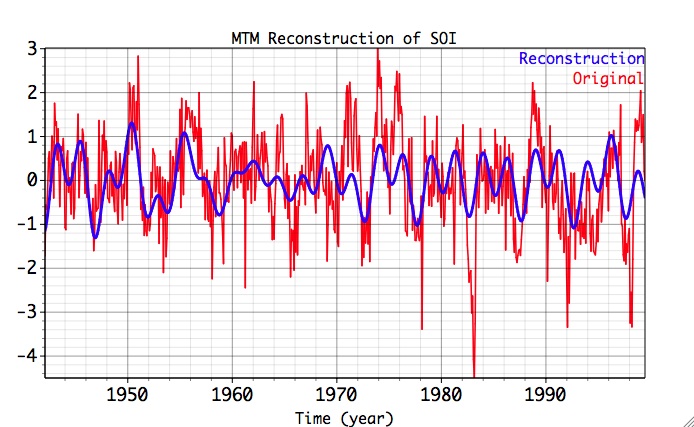
By selecting the Coherence check box, user can choose a 2nd vector to compute MTM coherence with the Data vector, and store it in MTM results. Both vectors should have the same length, and the coherence will be computed with the specified number of tapers, resolution, and other relevant settings. Below are shown Coherence estimates of original SOI with MTM-filtered series,

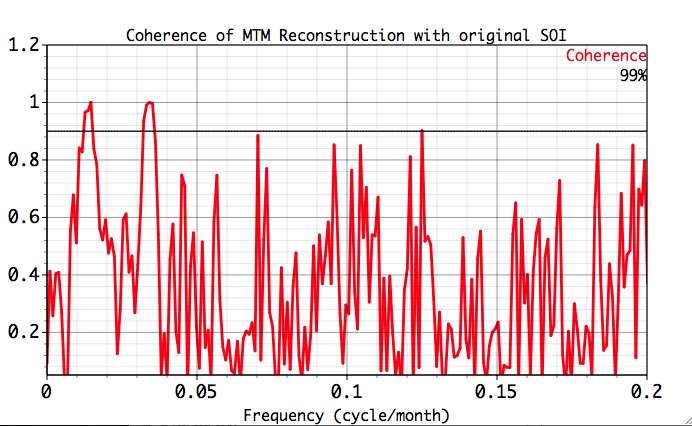
and SSA-filtered series:

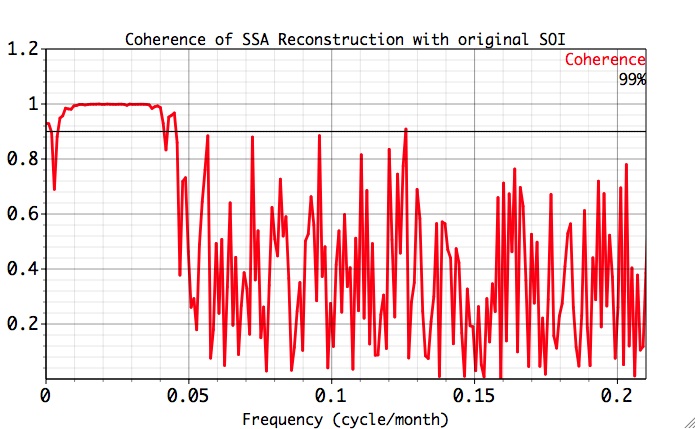
As also indicated by the MTM Components table,

SSA reconstruction provides for a very high coherence in a much wider frequency band then MTM, which is mainly restricted to the frequencies used in the reconstruction. This result is an agreement with the Blackman-Tukey cross-spectrum of SSA-filtered time series and original SOI, and also demonstrates SSA use as a very effective frequency band filter.