2. THEORY

Blackman-Tukey Correlogram and Cross-Spectrum

Both periodograms and correlograms are usually performed on weighted versions of the time series or autocorrelation functions in order to reduce power leakage (artificially high power estimates at frequencies away from the true peak frequencies). Press et al. (1989, pp. 423-424) note that "when we select a run of N sampled points for periodogram spectral estimation, we are in effect multiplying an infinite run of ... data ... by a window function in time, one which is zero except during the total sampling time [NDt], and is unity during that time." The sharp edges of this window function contain much power at highest frequencies, which is imparted to the windowed signal and leads to power leakage. A similar argument can be made for correlograms. Weighting the data or correlation function by various tapered shapes (high in center and falling off to sides) is an accepted traditional approach to reducing power leakage.

In the Blackman-Tukey approach P_X(f) is estimated by

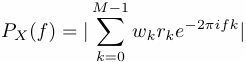
where r_k is the autocorrelation estimate at lag k, M is the maximum lag considered and window length, and w_k is the windowing function. Several window shapes are available in the Toolkit: Bartlett (triangular), Hamming (cosinusoidal), Hanning (slightly different cosinusoidal), and none.

You may find that the various windows of the same widths give similar results. The more important choice is how wide the windows should be. The averaging associated with windowing a series reduces the resolution of the methods, from the frequency intervals of 1/N, to a windowed frequency intervals of about 1/M (e.g., Kay 1988, p. 81). Thus, wider windows yield higher spectral resolution, and vice versa.

However, there is a trade-off between higher resolution and increasing variance of the spectral estimate. At the extreme, a single (M=N) direct application of FFT to an unwindowed time series results in a periodogram with a theoretical standard deviation of the estimates equal to the estimates at each frequency, regardless of the number of observations in the time series (Press et al. 1989, p. 423). Averaging the results from many short data windows throughout the series (or autocorrelation) effectively increases the number of independent samples used in estimation and thereby reduces the estimation variance. Kay (1988, section 4.5) shows that the variance of a power spectrum obtained by a windowed correlogram is 2M/3N of the estimated power at each frequency. Thus a narrower window should be used to smooth the spectrum and reduce the sampling errors on the estimate. In practice, Kay (1988) recommends that windows should be no more than one-fifth to one-tenth the total number of data points (to obtain desired estimate-variance reductions) and not too much smaller (in order to retain the ability to distinguish between powers at neighboring frequencies and to obtain the desired leakage reductions).

Theoretical estimates of variance for Blackman-Tukey power spectra are available (e.g., Kay, 1988) and the Toolkit provides error bars constructed from them. These can either be plotted about the estimates themselves, or as a red-noise uncertainty interval. In the latter case, an AR(1) process is fitted to the data, and the the error bars are centered on the theoretical AR(1) spectrum.

As a "traditional" method, the correlogram is intended to provide a familiar benchmark against which the other more modern methods provided in the Toolkit can be judged.

Cross-Spectra

Blackman-Tukey correlogram provides a straightforward way to compute the cross-power spectrum P_XY of the two input signals x(t) and y(t):

where X(f) and Y(f) are the correlogram estimates of the individual time series x(t) and y(t).

Cross-power spectrum can be used to estimate coherence between the two signals. However it requires averaging of spectral estimates of independent realizations of x(t) and y(t). Multi-taper method provides a practical way to compute Coherence by averaging the individual spectra given by each tapered version of the data.

Multi-channel SSA is an advanced, data-adaptive method to analyze oscillatory spatio-temporal modes in multivariate time series. In addition to identifying oscillatory peaks in the cross-spectrum, MSSA allows reconstruction of the multivariate oscillatory modes.

References

1. Blackman, R.B., and Tukey, J.,W., 1958: The measurement of power spectra from the point of view of communication engineering. Dover Publications, 190 pp.

2. Kay, S.M., 1988: Modern spectral estimation--Theory and application. Prentice-Hall, 543 pp

3, Percival, D.B., and Walden, A.T., 1993: Spectral analysis for physical applications--Multitaper and conventional univariate techniques. Cambridge University, 580 pp.

4. Press, W.H., Flannery, B.P., Teukolsky, S.A., and Vetterling, W.T., 1989: Numerical recipes--The art of scientific computing. Cambridge University Press, 702 pp.